Logistic Regression#
Environment setup#
import platform
print(f"Python version: {platform.python_version()}")
assert platform.python_version_tuple() >= ("3", "6")
import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.colors import ListedColormap
import seaborn as sns
Python version: 3.7.5
# Setup plots
%matplotlib inline
plt.rcParams["figure.figsize"] = 10, 8
%config InlineBackend.figure_format = 'retina'
sns.set()
import sklearn
print(f"scikit-learn version: {sklearn.__version__}")
assert sklearn.__version__ >= "0.20"
from sklearn.datasets import make_classification, make_blobs
from sklearn.linear_model import SGDClassifier, LogisticRegression
from sklearn.metrics import classification_report
scikit-learn version: 0.22.1
Show code cell source
def plot_data(x, y):
"""Plot some 2D data"""
fig, ax = plt.subplots()
scatter = ax.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu)
legend1 = ax.legend(*scatter.legend_elements(),
loc="lower right", title="Classes")
ax.add_artist(legend1)
plt.xlim((min(x[:, 0]) - 0.1, max(x[:, 0]) + 0.1))
plt.ylim((min(x[:, 1]) - 0.1, max(x[:, 1]) + 0.1))
def plot_decision_boundary(pred_func, x, y, figure=None):
"""Plot a decision boundary"""
if figure is None: # If no figure is given, create a new one
plt.figure()
# Set min and max values and give it some padding
x_min, x_max = x[:, 0].min() - 0.5, x[:, 0].max() + 0.5
y_min, y_max = x[:, 1].min() - 0.5, x[:, 1].max() + 0.5
h = 0.01
# Generate a grid of points with distance h between them
xx, yy = np.meshgrid(np.arange(x_min, x_max, h), np.arange(y_min, y_max, h))
# Predict the function value for the whole grid
Z = pred_func(np.c_[xx.ravel(), yy.ravel()])
Z = Z.reshape(xx.shape)
# Plot the contour and training examples
plt.contourf(xx, yy, Z, cmap=plt.cm.Spectral)
cm_bright = ListedColormap(["#FF0000", "#00FF00", "#0000FF"])
plt.scatter(x[:, 0], x[:, 1], c=y, s=40, cmap=plt.cm.RdYlBu, alpha=0.8)
Binary classification#
Problem formulation#
Logistic regression is a classification algorithm used to estimate the probability that a data sample belongs to a particular class.
A logistic regression model computes a weighted sum of the input features (plus a bias term), then applies the logistic function to this sum in order to output a probability.
The function output is thresholded to form the model’s prediction:
\(0\) if \(y' \lt 0.5\)
\(1\) if \(y' \geqslant 0.5\)
Loss function: Binary Crossentropy (log loss)#
See loss definition for details.
Model training#
No analytical solution because of the non-linear \(\sigma()\) function: gradient descent is the only option.
Since the loss function is convex, GD (with the right hyperparameters) is guaranteed to find the global loss minimum.
Different GD optimizers exist: newton-cg, l-bfgs, sag… Stochastic gradient descent is another possibility, efficient for large numbers of samples and features.
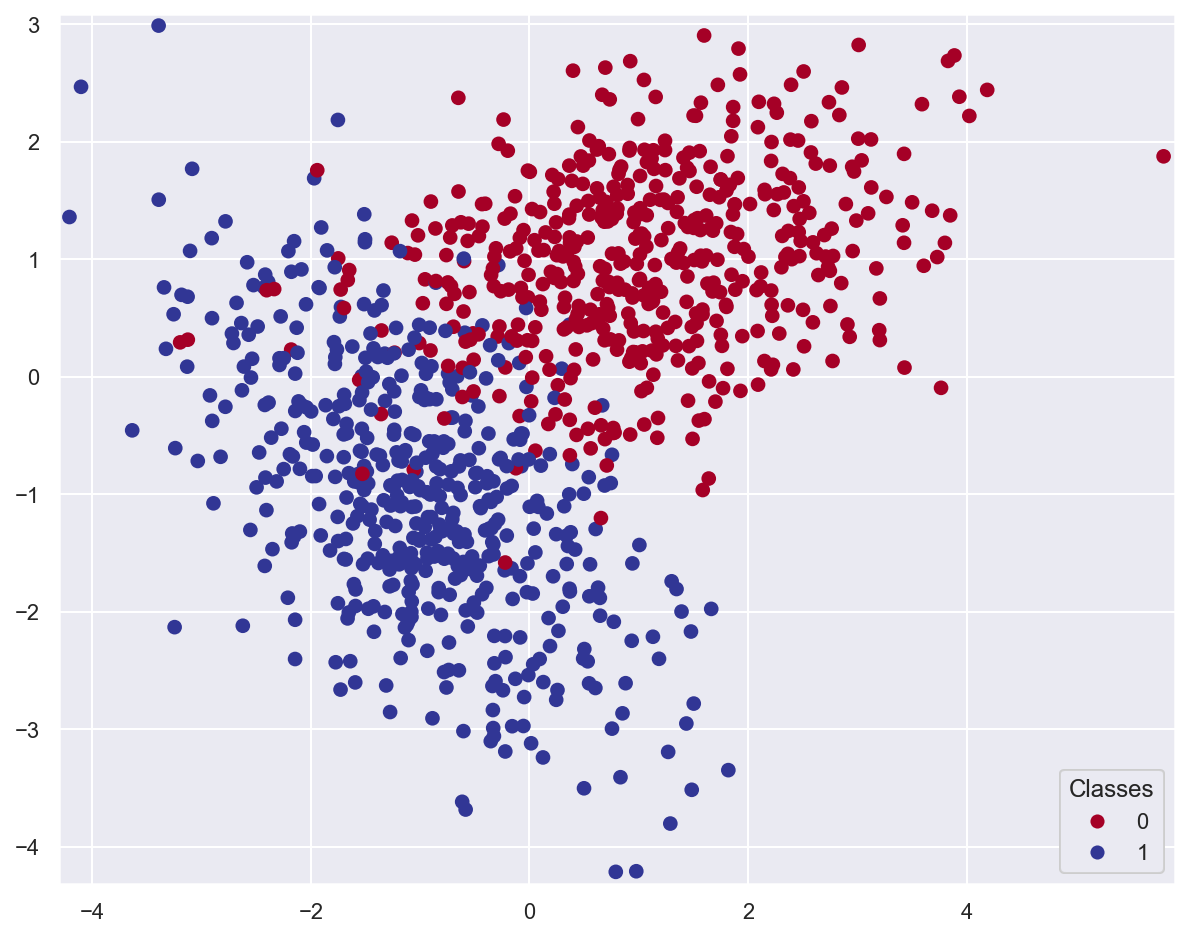
Example: classify planar data#
# Generate 2 classes of linearly separable data
x_train, y_train = make_classification(
n_samples=1000,
n_features=2,
n_redundant=0,
n_informative=2,
random_state=26,
n_clusters_per_class=1,
)
plot_data(x_train, y_train)
# Create a Logistic Regression model based on stochastic gradient descent
# Alternative: using the LogisticRegression class which implements many GD optimizers
lr_model = SGDClassifier(loss="log")
# Train the model
lr_model.fit(x_train, y_train)
print(f"Model weights: {lr_model.coef_}, bias: {lr_model.intercept_}")
Model weights: [[-2.96719034 -2.55668143]], bias: [-0.57585284]
# Print report with classification metrics
print(classification_report(y_train, lr_model.predict(x_train)))
precision recall f1-score support
0 0.96 0.92 0.94 502
1 0.92 0.96 0.94 498
accuracy 0.94 1000
macro avg 0.94 0.94 0.94 1000
weighted avg 0.94 0.94 0.94 1000
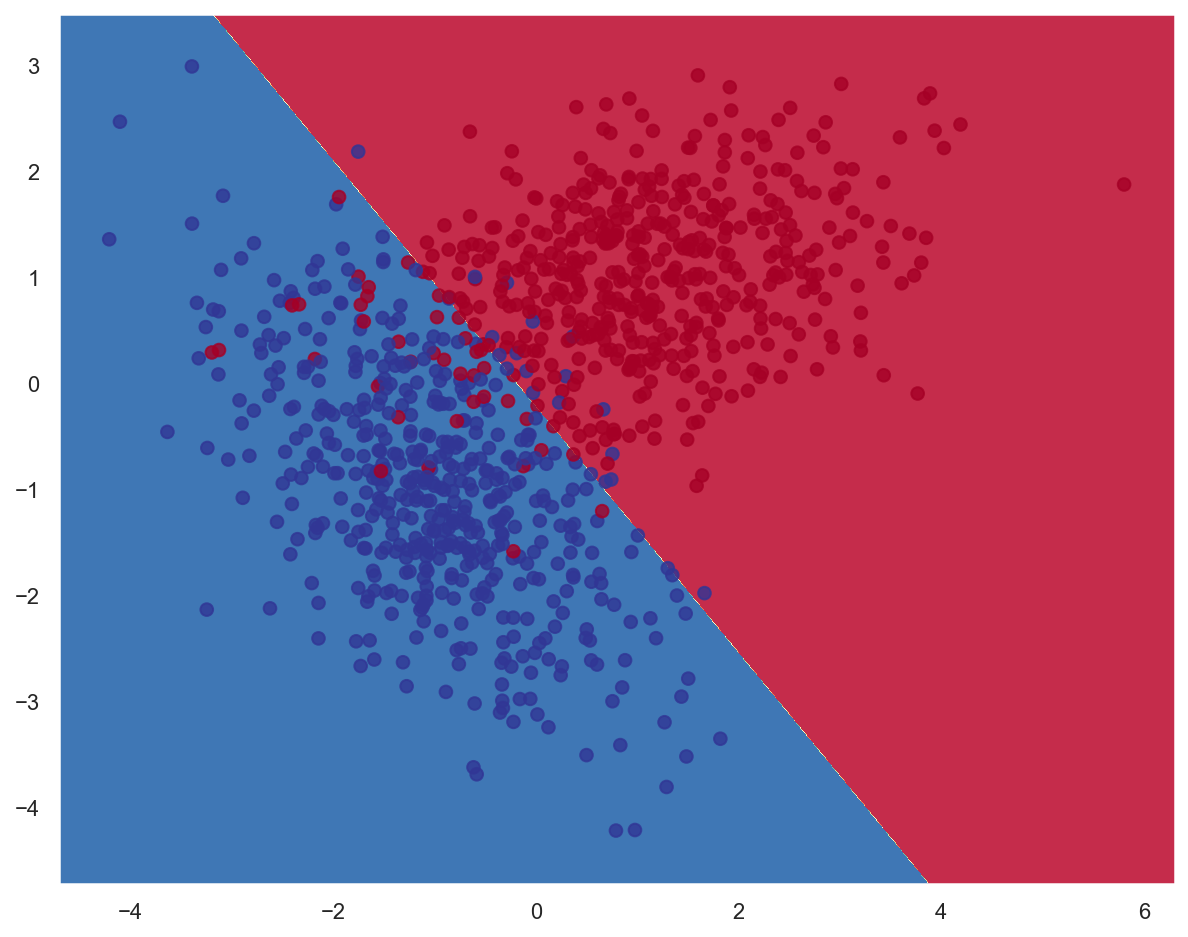
# Plot decision boundary
plot_decision_boundary(lambda x: lr_model.predict(x), x_train, y_train)
Multivariate regression#
Problem formulation#
Multivariate regression, also called softmax regression, is a generalization of logistic regression for multiclass classification.
A softmax regression model computes the scores \(s_k(\pmb{x})\) for each class \(k\), then estimates probabilities for each class by applying the softmax function to compute a probability distribution.
For a sample \(\pmb{x}^{(i)}\), the model predicts the class \(k\) that has the highest probability.
Each class \(k\) has its own parameter vector \(\pmb{\theta}^{(k)}\).
Model output#
\(\pmb{y}^{(i)}\) (ground truth): binary vector of \(K\) values. \(y^{(i)}_k\) is equal to 1 if the \(i\)th sample’s class corresponds to \(k\), 0 otherwise.
\(\pmb{y}'^{(i)}\): probability vector of \(K\) values, computed by the model. \(y'^{(i)}_k\) represents the probability that the \(i\)th sample belongs to class \(k\).
Loss function: Categorical Crossentropy#
See loss definition for details.
Model training#
Via gradient descent:
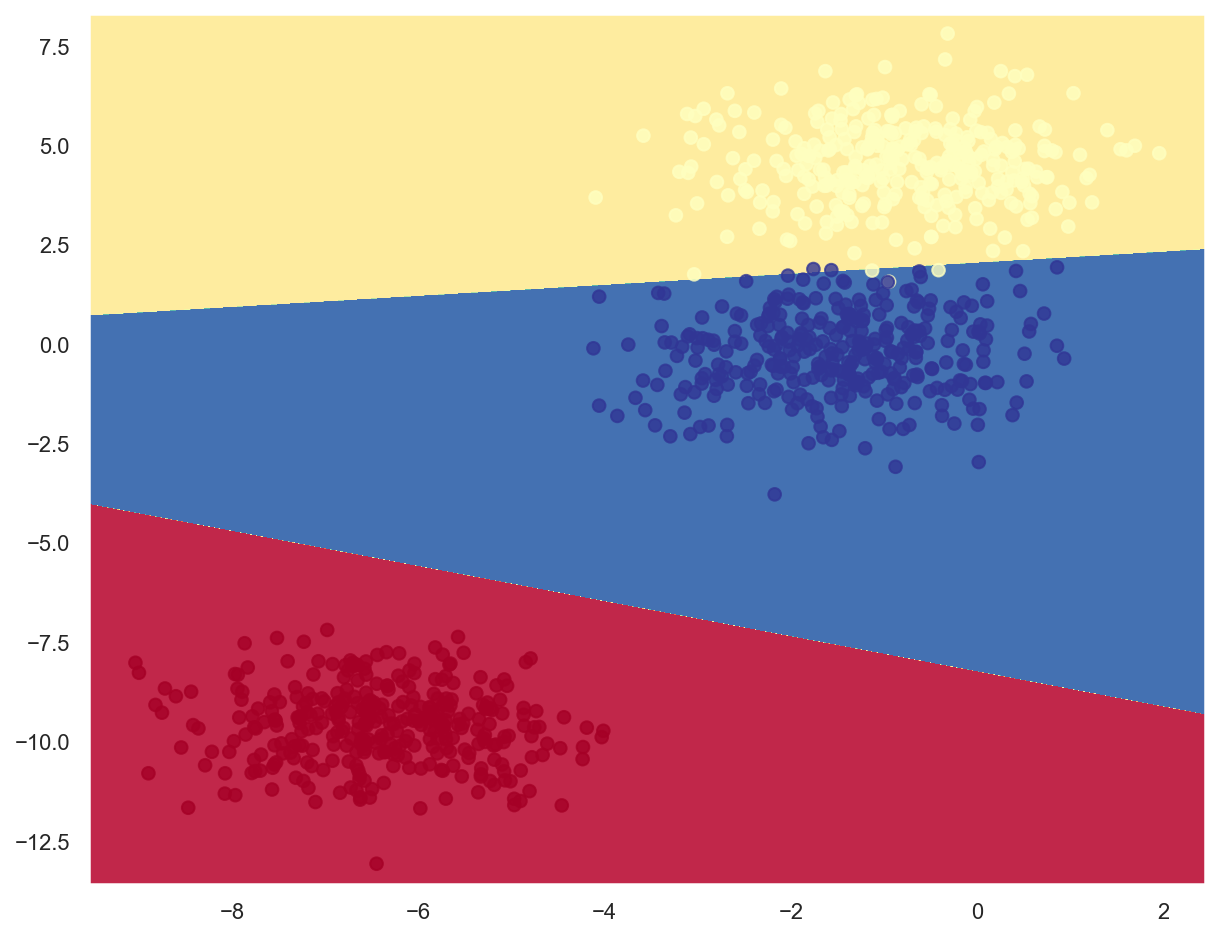
Example: classify multiclass planar data#
# Generate 3 classes of linearly separable data
x_train_multi, y_train_multi = make_blobs(n_samples=1000, n_features=2, centers=3, random_state=11)
plot_data(x_train_multi, y_train_multi)
# Create a Logistic Regression model based on stochastic gradient descent
# Alternative: using LogisticRegression(multi_class="multinomial") which implements SR
lr_model_multi = SGDClassifier(loss="log")
# Train the model
lr_model_multi.fit(x_train_multi, y_train_multi)
print(f"Model weights: {lr_model_multi.coef_}, bias: {lr_model_multi.intercept_}")
Model weights: [[ -5.76624648 -17.43149458]
[ -1.27339599 19.17812979]
[ 1.5231193 -0.91647832]], bias: [-133.15588019 -38.36388245 2.53712564]
# Print report with classification metrics
print(classification_report(y_train_multi, lr_model_multi.predict(x_train_multi)))
precision recall f1-score support
0 1.00 1.00 1.00 334
1 0.99 0.99 0.99 333
2 0.99 0.99 0.99 333
accuracy 0.99 1000
macro avg 0.99 0.99 0.99 1000
weighted avg 1.00 0.99 0.99 1000
# Plot decision boundaries
plot_decision_boundary(lambda x: lr_model_multi.predict(x), x_train_multi, y_train_multi)